- 딥러닝에서의 데이터표현
- 텐서: 데이터를 위한 컨테이너, 임의의 차원 개수를 가지는 행렬의 일반화된 모습, 차원을 종종 축이라고 부름
- 스칼라(0D 텐서): 하나의 숫자만 담음, 축의 개수는 0
- 벡터(1D 텐서): 숫자의 배열을 벡터 또는 1D 텐서라고 부름, 하나의 축
- 행렬(2D 텐서): 벡터의 배열이 행렬 또는 2D 텐서, 2개의 축, 숫자가 채워진 사각 격자라고 생각할 수 있음
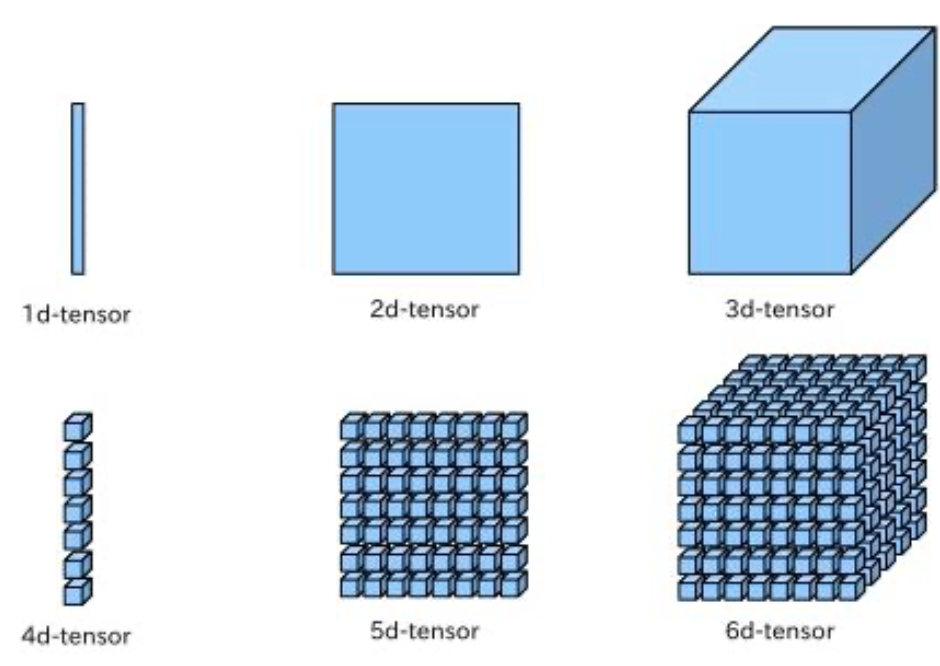
- 3D텐서와 고차원텐서
- 행렬들을 하나의 새로운 배려로 합치면 숫자가 채워진 직육면체 형태로 해석할 수 있는 3D텐서가 만들어짐
- 3D텐서들을 하나의 배열로 합치면 4D 텐서를 만드닌 식으로 이어짐
- 딥러닝에서는 보통 0D에서 4D까지 텐서를 다루며, 동영상 데이터는 5D 텐서까지 가기도 함
- 텐서의 예시
- 벡터 데이터: (samples, features), 나이/우편번호/소득으로 구성된 인구 통계 데이터
- 시계열 데이터 또는 시퀀스 데이터: (samples, timesteps, features), 주식 가격 데이터셋, 트윗 데이터셋
- 이미지: (samples, height, width, channels), 높이/너비/컬러 채널
- 비디오 데이터: (samples, frames, height, width, channels), 비디오는 프레임의 연속이고 각 프레임은 하나의 컬러 이미지
- 텐서 연산
- 원소별 연산: 각각의 원소에 대해 독립적으로 적용되는 연산
- 하나의 텐서에 대해 이루어지는 텐서 연산의 예시: relu 연산
- 복수의 텐서에 대해 이루어지는 텐서 연산의 예시: 덧셈 연산
- 브로드 캐스팅: 차원이 맞지 않는 텐서에 대해 연산을 수행하고자 할때 발생하는 가상 연산
- 큰 텐서의 차원에 맞도록 크기가 작은 텐서에 새로운 축(broadcasting 축)이 추가됨
- 새 축을 따라서 큰 텐서의 크기와 맞을 때까지 작은 텐서를 확장함
- 하나의 텐서만 늘리는 것이 아니라, 두 개의 텐서를 동시에 브로드캐스팅하는 것도 가능함
- 단, 차원을 줄이는 방향으로는 일어날 수 없음
- 텐서 점곱: 원소별 연산 곱셈이 아닌, 입력 텐서의 원소들을 결합시키는 연산 (행렬 곱셈과 유사)
- 텐서 크기 변환: 특정 크기에 맞추어 행과 열을 재배열하는 연산으로사, 크기가 변화된 텐서는 원래 텐서와 원소 개수가 동일함
- 텐서 연산 및 딥러닝의 기하학적 해석
- 텐서의 내용은 기하학적 공간 상의 좌표점으로 해석 가능함
- 신경망은 텐서 연산들의 연쇄를 통해 구성되어있으며, 모든 텐서 연산은 입력 데이터에 대한 기하학적 변환으로 해석될 수 있음
- 기계 학습은 복잡한 데이터의 매니폴드에 대한 깔끔한 표현을 찾는 것을 목표로 함
- 딥러닝은 이 과정에서 기초적인 연산들을 길게 연결하여 복잡한 기하학적 변환을 조금씩 분해하는 접근을 수행함
- 원소별 연산: 각각의 원소에 대해 독립적으로 적용되는 연산

- 그래디언트 기반 최적화
- 그래디언트 값이 큰 입력 값의 변화는 함수 값에 대해서도 큰 변화를 야기하며, 그래디언트의 방향과 크기를 고려하여 입력 값을 이동시키는 것이 효율적임, 반복적으로 입력 값을 이동시키며 속성 공간에 대한 탐색을 수행할 수 있음
- 신경망 학습에 대한 적용
- 손실에 대한 매개 변수의 그래디언트를 이용하여 손실에 대한 영향력을 알 수 있음
- 매개 변수 집합의 그래디언트의 반대 방향으로 이동하면 손실은 감소함
- 이를 신경망 훈련 과정에 적용할 수 있음
- 네트워크의 매개 변수 (w, b)에 대한 손실 함수의 그래디언트를 계산함
- 그래디언트의 반대 방향으로 매개 변수를 조금 이동시킴
- 이때, 매겨 변수를 얼마나 변화시킬지 결정하는 학습률이 수렴 속도를 결정함
- 현재 그래디언트 값에 대해서만 고려한 학습은 지역 최적해에 수렴하는 문제가 있음
- 이러한 문제를 해결하기 위해서는 이전에 업데이트한 매겨 변수의 정보를 함께 고려하여 현재 매개 변수의 값을 업데이트할 필요가 있음
- 변화율 연결을 위한 역전파 알고리즘
- 최종 손실 값에서부터 시작하여 각각의 매개 변수가 기여한 정도를 계산하고 역방향으로 매개 변수를 업데이트함
- 출력 값과 실제 클래스 정보 값을 비교하여 오류 계산
- 가중치의 변화량을 이용하여 가중치들을 갱신함


'데이터사이언스' 카테고리의 다른 글
| 신경망 모델 (신경망 모형) (0) | 2019.10.24 |
|---|---|
| 신경망 모델 (퍼셉트론 모형) (0) | 2019.10.24 |
| 딥러닝의 필요성 (0) | 2019.10.22 |
| 머신러닝/딥러닝의 역사 (0) | 2019.10.22 |
| 인공지능과 머신러닝 그리고 딥러닝 소개 (0) | 2019.10.22 |



