회귀계수를 축소하는 이유
- 영향력이 없는 입력 변수의 계수를 0에 가깝게 가져간다면, 모형에 포함되는 입력 변수의 수를 줄일 수 있음
- 입력 변수의 수를 줄였을때의 장점
- 잡음(noise)를 제거해 모형의 정확도를 개선함
- 모형의 연산 속도가 빨라짐
- 다중공선성의 문제를 제거해 모형의 해석 능력을 향상시킴
- 예를들어 입력 변수가 나이, 생년이 있는경우 둘은 같은 의미를 갖기 때문에 하나를 제거함
- 계수축소법에는 Ridge와 LASSO 방법이 있음
Ridge regression
- Rigde 회귀에서는 f(beta)에 회귀계수의 제곱의 합을 대입함
- λ(람다)는 tuning parameter로 크면 클 수록 보다 많은 회귀계수를 0으로 수렴시킴
- 적절한 λ의 값은 데이터마다 달라짐
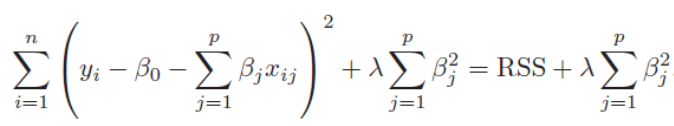
LASSO(Least Absolute Shrinkage and Selection Operator) regression
- LASSO 회귀에서는 f(beta)에 회귀계수의 절대값의 합을 대입함
- λ(람다)는 tuning parameter로 크면 클 수록 보다 많은 회귀계수를 0으로 수렴시킴

공통점
- 계수축소법으로 잔차와 회귀계수를 최소화하는 최적화 문제임
- 즉 min SSE + f(beta)의 목적함수를 푸는 문제임
차이점
- Ridge는 계수가 0에 가깝게 축소되는데 비해 LASSO는 계수가 0으로 축소됨
- Rigde는 입력 변수들이 전반적으로 비슷한 수준으로 출력 변수에 영향을 미치는 경우에 사용함
- LASSO는 출력 변수에 미치는 입력 변수의 영향력 편차가 큰 경우에 사용함

'데이터사이언스' 카테고리의 다른 글
| SVM의 개념 (0) | 2019.06.21 |
|---|---|
| 선형회귀의 적합성 평가와 과적합을 판단하는 방법 (0) | 2019.06.20 |
| 다중선형회귀에서 다중공선성 문제와 해결방법 (0) | 2019.06.20 |
| 분류 모형 성능 지표 (제1종 오류, 제2종 오류, 정확도, 정밀도, 재현율, 특이도) (1) | 2019.06.19 |
| 분산과 편파성의 트레이드오프 (0) | 2019.06.18 |



